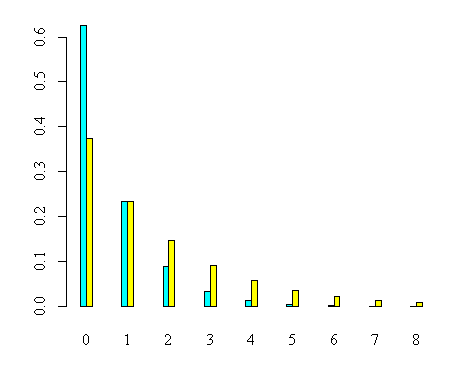
Si considera variabile aleatoria Z = "l'evento si verifica per la prima volta alla n-esima prova". La sua distribuzione di probabilità, detta distribuzione geometrica, è fornita dalla seguente formula (dove p indica la probabilità costante del successo e q=1-p la probabilità dell'insuccesso):
La probabilità di un primo successo alla n-esima prova è infatti il prodotto di p, probabilità di successo, per q, probabilità di n insuccessi consecutivi.
Può risultare utile un esempio chiarificatore:
Si ha un'urna composta da 10 palline bianche e 6 palline nere. Studiare le variabili aleatorie Z e W che contano il numero delle prove necessarie per ottenere una prima volta l'estrazione di una pallina rispettivamente bianca o nera.
La probabilità di estrarre una pallina bianca è p=10/16=5/8, mentre quella di estrarre una pallina nera è q=1-p=3/8. I ruoli di p e q si scambiano nelle due situazioni e per le variabili aleatorie Z e W si hanno le seguenti rispettive leggi valide per n>=1:
p(Z = n) = 5/8 × (3/8)n
p(W = n) = 3/8 × (5/8)n
La rappresentazione grafica di queste distribuzioni è la seguente:
Ritorna alla pagina principale.
Ritorna alla homepage di Lorenzo Azzalini.